I have owned a copy of - Causal Inference in Python a couple of years ago, but never opened it.

I finally decided to crack it open to go over Double Machine Learning, but something caught my eye in the Frisch-Waugh-Lovell Theorem and Orthogonalization section, so I gave it a read. This was the best treatment of this material I have ever seen!

It presented it so well, anything I could write wouldn't be as good. But a highlight for me was the revelation that I really didn't understand it all along. I mean, sure, I knew the premise...

The standard setup is the familiar model

$Y_i = \beta_0 + \beta_1 X_i + \gamma Z_i + u_i$

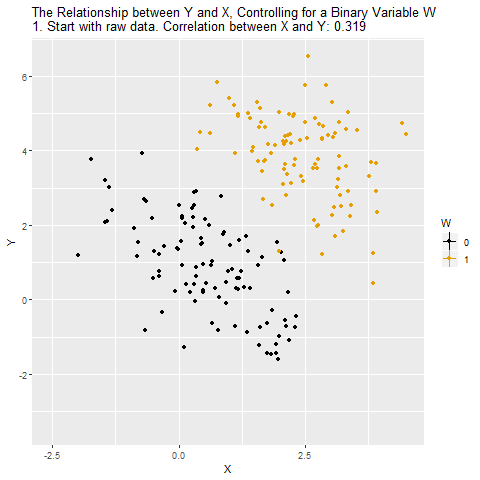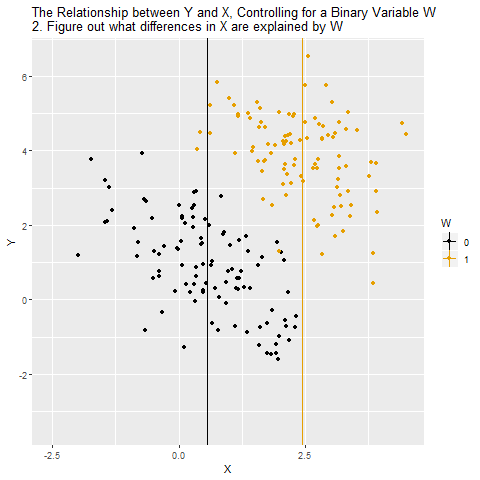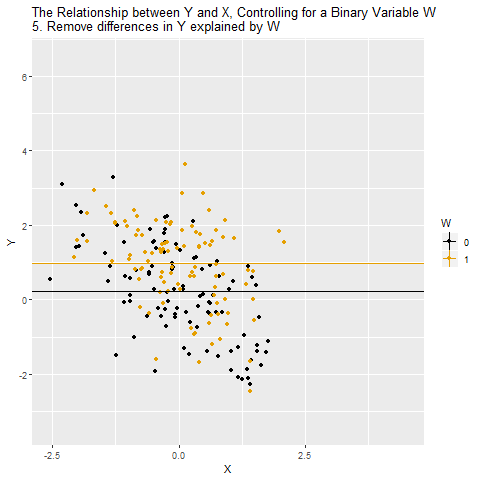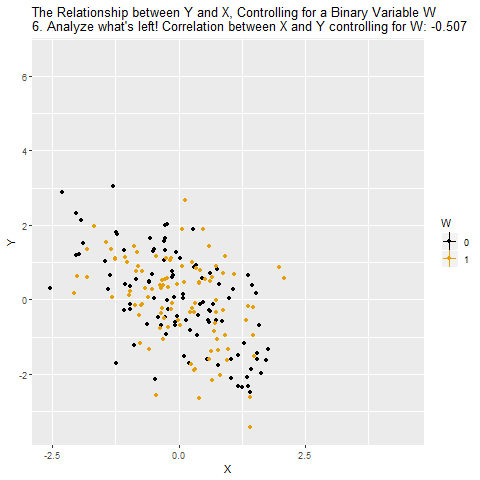
where $X_i$ is the variable of interest and $Z_i$ is a control. The FWL theorem says that you get the exact same $\hat\beta_1$ by doing three regressions: regress $X_i$ on $Z_i$ and save the residuals, regress $Y_i$ on $Z_i$ and save those residuals, and then regress one set of residuals on the other. I’ve known that result for years and I simply accepted it as a useful fact.

What clicked for me in this treatment is that the two partialling-out steps are not doing the same thing. They look symmetric, but they serve different purposes. When you regress $X_i$ on $Z_i$, you’re removing the part of $X_i$ that is explained by the controls. That step is what eliminates omitted-variable bias in the coefficient on $X_i$. When you regress $Y_i$ on $Z_i$, you’re removing variation in the outcome that is explained by the controls. That step reduces noise, not bias.

The part I had never fully appreciated is that you only need the first step to get an unbiased estimate of $\beta_1$. If you take the residuals from the regression of $X_i$ on $Z_i$ and plug those straight into the full model, you still get the correct $\hat\beta_1$. Skipping the residualization of $Y_i$ only affects the standard errors, not the point estimate.

I don't feel TOO bad for not understanding. Most standard treatments never emphasize this asymmetry. They show the algebra, note the equivalence, and move on. Seeing the distinction laid out made the logic of orthogonalization suddenly much cleaner, especially in light of modern causal ML methods that build directly on this idea.

Although, perhaps it should have clicked when I saw Nick Huntington-Klein's animations 6 years ago or so (from https://nickchk.com/causalgraphs.html):